Hashi:Linkdoku Bridges Puzzle Hack 4.5.0 + Redeem Codes
Connect Islands with Bridges
Developer: 建明 顾
Category: Games
Price: Free
Version: 4.5.0
ID: com.iyond.game.hashi
Screenshots
Description
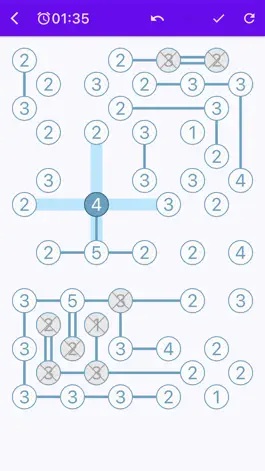
In Hashiwokakero(hashi, chopsticks, bridges) you are the king of the islands, and your job is to connect the islands according to their populations – small islands need only one bridge (it says 1 in the island), and larger islands need more bridges (the number in the island). Then remember that this is all one kingdom, yours, so you must make it possible for all the citizens to travel between all the islands. Also known as Bridges/Chopsticks
RULES:
1. Connect islands (the circles with numbers) with as many bridges as the number in the island.
2. There can be no more than two bridges between two islands.
3. Bridges cannot go across islands or other bridges.
4. The bridges will form a continuous link between all the islands.
Features:
* 720 free Classic hashi puzzles
* Extra 480 bonus puzzles published free each month
* Multiple sizes, from 6x9 to 14x21
* Connectable Island hint
* Highlights connected islands
* Undo / Redo
* Automatically saved
* Snapshots for complex puzzles
* Backup & restore puzzle progress to Cloud
* Multiple beautiful themes
* Multiple languages support
* Timer
Solution methods:
Solving a Hashiwokakero puzzle is a matter of procedural force: having determined where a bridge must be placed, placing it there can eliminate other possible places for bridges, forcing the placement of another bridge, and so on.
An island showing '3' in a corner, '5' along the outside edge, or '7' anywhere must have at least one bridge radiating from it in each valid direction, for if one direction did not have a bridge, even if all other directions sported two bridges, not enough will have been placed. A '4' in a corner, '6' along the border, or '8' anywhere must have two bridges in each direction. This can be generalized as added bridges obstruct routes: a '3' that can only be travelled from vertically must have at least one bridge each for up and down, for example.
It is common practice to cross off or fill in islands whose bridge quota has been reached. In addition to reducing mistakes, this can also help locate potential "short circuits": keeping in mind that all islands must be connected by one network of bridges, a bridge that would create a closed network that no further bridges could be added to can only be permitted if it immediately yields the solution to the complete puzzle. The simplest example of this is two islands showing '1' aligned with each other; unless they are the only two islands in the puzzle, they cannot be connected by a bridge, as that would complete a network that cannot be added to, and would therefore force those two islands to be unreachable by any others.
Any bridge that would completely isolate a group of islands from another group would not be permitted, as one would then have two groups of islands that could not connect. This deduction, however, is not very commonly seen in Hashiwokakero puzzles.
Determining whether a Hashiwokakero puzzle has a solution is NP-complete, by a reduction from finding Hamiltonian cycles in integer-coordinate unit distance graphs. There is a solution using integer linear programming in the MathProg examples included in GLPK. A library of puzzles counting up to 400 islands as well as integer linear programming results are also reported.
RULES:
1. Connect islands (the circles with numbers) with as many bridges as the number in the island.
2. There can be no more than two bridges between two islands.
3. Bridges cannot go across islands or other bridges.
4. The bridges will form a continuous link between all the islands.
Features:
* 720 free Classic hashi puzzles
* Extra 480 bonus puzzles published free each month
* Multiple sizes, from 6x9 to 14x21
* Connectable Island hint
* Highlights connected islands
* Undo / Redo
* Automatically saved
* Snapshots for complex puzzles
* Backup & restore puzzle progress to Cloud
* Multiple beautiful themes
* Multiple languages support
* Timer
Solution methods:
Solving a Hashiwokakero puzzle is a matter of procedural force: having determined where a bridge must be placed, placing it there can eliminate other possible places for bridges, forcing the placement of another bridge, and so on.
An island showing '3' in a corner, '5' along the outside edge, or '7' anywhere must have at least one bridge radiating from it in each valid direction, for if one direction did not have a bridge, even if all other directions sported two bridges, not enough will have been placed. A '4' in a corner, '6' along the border, or '8' anywhere must have two bridges in each direction. This can be generalized as added bridges obstruct routes: a '3' that can only be travelled from vertically must have at least one bridge each for up and down, for example.
It is common practice to cross off or fill in islands whose bridge quota has been reached. In addition to reducing mistakes, this can also help locate potential "short circuits": keeping in mind that all islands must be connected by one network of bridges, a bridge that would create a closed network that no further bridges could be added to can only be permitted if it immediately yields the solution to the complete puzzle. The simplest example of this is two islands showing '1' aligned with each other; unless they are the only two islands in the puzzle, they cannot be connected by a bridge, as that would complete a network that cannot be added to, and would therefore force those two islands to be unreachable by any others.
Any bridge that would completely isolate a group of islands from another group would not be permitted, as one would then have two groups of islands that could not connect. This deduction, however, is not very commonly seen in Hashiwokakero puzzles.
Determining whether a Hashiwokakero puzzle has a solution is NP-complete, by a reduction from finding Hamiltonian cycles in integer-coordinate unit distance graphs. There is a solution using integer linear programming in the MathProg examples included in GLPK. A library of puzzles counting up to 400 islands as well as integer linear programming results are also reported.
Version history
4.5.0
2023-07-08
+ July 2023 update package
+ Imporvements and fixes
+ Imporvements and fixes
4.4.4
2023-03-06
+ Backup & restore puzzle progress to Cloud
+ March 2023 update package, include 480 puzzles
+ improves performance and stability
+ March 2023 update package, include 480 puzzles
+ improves performance and stability
4.3.1
2023-01-30
+ February 2023 Update Pack, Happy Chinese New Year
+ Support snapshot function, they will help you solve complex puzzles more conveniently
+ Support snapshot function, they will help you solve complex puzzles more conveniently
4.2.3
2023-01-17
+ Support snapshot function, they will help you solve complex puzzles more conveniently
+ More methods to unlock puzzles
+ More methods to unlock puzzles
4.2.0
2023-01-15
+ Support snapshot function, they will help you solve complex puzzles more conveniently
4.1.3
2022-12-28
+ January Update, 30 puzzles each level, 30 plus for subscribers. Happy new year!
4.0.6
2022-12-26
+ December Update, 30 puzzles each size
+ Improvements and fixes
+ Improvements and fixes
2.1.2
2022-08-14
Cheat Codes for In-App Purchases
| Item | Price | iPhone/iPad | Android |
|---|---|---|---|
| Monthly Subscriber (Ad free & Got double coins when buying) |
Free |
FH897982711✱✱✱✱✱ | 8510BBC✱✱✱✱✱ |
| Buy 600 game coins (Got 600 game coins after buying) |
Free |
FH534188745✱✱✱✱✱ | B2DC37C✱✱✱✱✱ |
| Buy 3600 game coins (Got 3600 game coins after buying) |
Free |
FH541133212✱✱✱✱✱ | E54FAB6✱✱✱✱✱ |
| Buy 1800 game coins (Got 1800 game coins after buying) |
Free |
FH110493459✱✱✱✱✱ | 43008DD✱✱✱✱✱ |
Ways to hack Hashi:Linkdoku Bridges Puzzle
- iGameGod (Watch Video Guide)
- iGameGuardian for iOS (Watch Video Guide) or GameGuardian for Android (Watch Video Guide)
- Lucky Patcher (Watch Video Guide)
- Cheat Engine (Watch Video Guide)
- Magisk Manager (Watch Video Guide)
- CreeHack (Watch Video Guide)
- Redeem codes (Get the Redeem codes)
Download hacked APK
Download Hashi:Linkdoku Bridges Puzzle MOD APK
Request a Hack
Ratings
5 out of 5
6 Ratings
Reviews
Ihsah,
Many levels
Many selections for the novice to the expert.