Numerical Tic Tac Toe Hack 1.0.1 + Redeem Codes

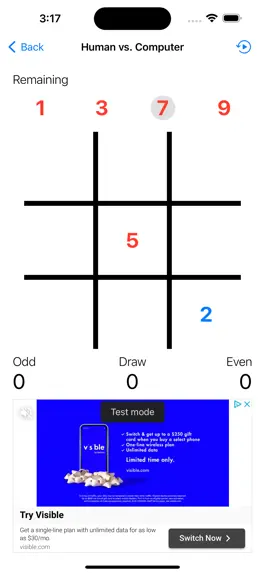
Numerical tic-tac-toe is a variant of tic-tac-toe that replaces the traditional Xs and Os with odd and even numbers. Players alternate placing numbers, aiming to form a line that adds up to 15. 

The game is played on a normal nine square tic-tac-toe board. The odd player begins with the numbers 1, 3, 5, 7, and 9. The even player begins with the numbers 2, 4, 6, and 8. Odd always goes first. The two sides alternate placing numbers on the board in empty squares.

Numbers cannot be repeated. So, there will only ever be a single instance of each number on the board. The first player to put a number down that achieves a sum of 15 composed of three numbers in a row, column, or diagonal wins the game. Note, that two numbers adding to 15 is not sufficient. So, a 6 next to a 9 is not a win.

*Features*
- Play against an AI opponent
- Play against a friend
- Three levels of difficulty
- Customizable colors

*History*
Numerical tic-tac-toe was invented in the late 1950s by American mathematician Ronald Graham. A similar game was contemporaneously invented by P.H. Nygaard.

In 1990, George Markowsy wrote a computer program that solved numerical tic-tac-toe. He proved that 1 in the top middle slot is a winning first move for odd. In other words, in perfect play, odd wins the game. Markowsky published his findings in The Journal of Recreational Mathematics.